Democratic classification of free-format survey responses with a network-based framework
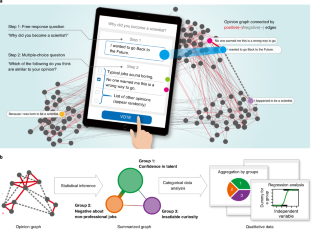
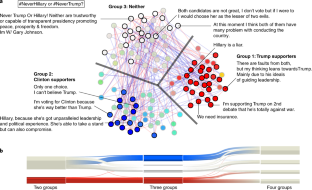
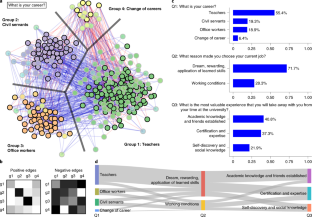
Social surveys have been widely used as a method of obtaining public opinion. Sometimes, it is more ideal to collect opinions by presenting questions in free-response formats than in multiple-choice formats. Despite their advantages, free-response questions are rarely used in practice because they usually require manual analysis. Therefore, classification of free-format texts can present a formidable task in large-scale surveys and can be influenced by the interpretation of analysts. In this study, we propose a network-based survey framework in which responses are automatically classified in a statistically principled manner. This can be achieved because, in addition to the text, similarities among responses are also assessed by each respondent. We demonstrate our approach using a poll on the 2016 US presidential election and a survey taken by graduates of a particular university. The proposed approach helps analysts interpret the underlying semantics of responses in large-scale surveys.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
133,45 € per year
only 11,12 € per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout
Similar content being viewed by others
A dataset on survey designs and quality of social and behavioral science surveys during the COVID-19 pandemic
Article Open access 12 June 2024

Continuous and binary sets of responses differ in the field
Article Open access 23 August 2022

Using Machine Learning to Uncover Hidden Heterogeneities in Survey Data
Article Open access 05 November 2019
Data availability
The network datasets that support the findings of this study are available in a GitHub repository at https://github.com/tatsuro-kawamoto/opinion_graphs. The graph clustering code that supports the findings of this study is available in a GitHub repository at https://github.com/tatsuro-kawamoto/graphBIX.
References
- Kahn, R. L. & Cannell, C. F. The Dynamics of Interviewing: Theory, Technique, and Cases (Wiley, 1957).
- Schuman, H. & Scott, J. Problems in the use of survey questions to measure public opinion. Science236, 957–959 (1987). ArticleGoogle Scholar
- Schuman, H. & Presser, S. Questions and Answers in Attitude Surveys: Experiments on Question Form, Wording, and Context (Sage, 1996).
- RePass, D. E. Issue salience and party choice. Am. Polit. Sci. Rev.65, 389–400 (1971). ArticleGoogle Scholar
- Kelley, S. Jr. Interpreting Eelections (Princeton Univ. Press, 2014).
- Geer, J. G. What do open-ended questions measure? Public Opin. Q.52, 365–371 (1988). ArticleGoogle Scholar
- Singleton, R. & Straits, B. C. Approaches to Social Research. 6th edn (Oxford Univ. Press, 2017).
- Schuman, H. The random probe: a technique for evaluating the validity of closed questions. Am. Sociol. Rev.31, 218–222 (1966). ArticleGoogle Scholar
- Lombard, M., Snyder-Duch, J. & Bracken, C. C. Content analysis in mass communication: assessment and reporting of intercoder reliability. Human Commun. Res.28, 587–604 (2002). ArticleGoogle Scholar
- Giddens, A. & Sutton, P. W. Sociology 7th edn (Polity Press, 2013).
- Aicher, C., Jacobs, A. Z. & Clauset, A. Learning latent block structure in weighted networks. J. Complex Netw.3, 221–248 (2015). ArticleMathSciNetGoogle Scholar
- Newman, M. E. J. Network structure from rich but noisy data. Nat. Phys.14, 542–545 (2018). ArticleGoogle Scholar
- Peixoto, T. P. Reconstructing networks with unknown and heterogeneous errors. Phys. Rev. X8, 041011 (2018). Google Scholar
- Rosvall, M. & Bergstrom, C. T. Mapping change in large networks. PLoS ONE5, 1–7 (2010). ArticleGoogle Scholar
- Kawamoto, T. & Kabashima, Y. Comparative analysis on the selection of number of clusters in community detection. Phys. Rev. E97, 022315 (2018). ArticleGoogle Scholar
- Danon, L., Díaz-Guilera, A., Duch, J. & Arenas, A. Comparing community structure identification. J. Stat. Mech.2005, P09008 (2005). ArticleGoogle Scholar
- Rand, W. M. Objective criteria for the evaluation of clustering methods. J. Am. Stat. Assoc.66, 846–850 (1971). ArticleGoogle Scholar
- Hubert, L. & Arabie, P. Comparing partitions. J. Classif.2, 193–218 (1985). ArticleGoogle Scholar
- Simon, A. F. & Xenos, M. Dimensional reduction of word-frequency data as a substitute for intersubjective content analysis. Polit. Anal.12, 63–75 (2004). ArticleGoogle Scholar
- Hopkins, D. J. & King, G. A method of automated nonparametric content analysis for social science. Am. J. Polit. Sci.54, 229–247 (2010). ArticleGoogle Scholar
- Roberts, M. E. et al. Structural topic models for open-ended survey responses. Am. J. Polit. Sci.58, 1064–1082 (2014). ArticleGoogle Scholar
- Benoit, K., Conway, D., Lauderdale, B. E., Laver, M. & Mikhaylov, S. Crowd-sourced text analysis: reproducible and agile production of political data. Am. Polit. Sci. Rev.110, 278–295 (2016). ArticleGoogle Scholar
- Lind, F., Gruber, M. & Boomgaarden, H. G. Content analysis by the crowd: assessing the usability of crowdsourcing for coding latent constructs. Commun. Methods Meas.11, 191–209 (2017). ArticleGoogle Scholar
- Jacobson, M. R., Whyte, C. E. & Azzam, T. Using crowdsourcing to code open-ended responses: a mixed methods approach. Am. J. Eval.39, 413–429 (2018). ArticleGoogle Scholar
- Decelle, A., Krzakala, F., Moore, C. & Zdeborová, L. Asymptotic analysis of the stochastic block model for modular networks and its algorithmic applications. Phys. Rev. E84, 066106 (2011). ArticleGoogle Scholar
- Moore, C. The computer science and physics of community detection: landscapes, phase transitions, and hardness. Preprint at https://arxiv.org/abs/1702.00467 (2017).
- Fishkin, J. S. When the People Speak: Deliberative Democracy and Public Consultation (Oxford Univ. Press, 2011).
- Holland, P. W., Laskey, K. B. & Leinhardt, S. Stochastic blockmodels: first steps. Soc. Netw.5, 109–137 (1983). ArticleMathSciNetGoogle Scholar
- Wang, Y. J. & Wong, G. Y. Stochastic blockmodels for directed graphs. J. Am. Stat. Assoc.82, 8–19 (1987). ArticleMathSciNetGoogle Scholar
- Karrer, B. & Newman, M. E. J. Stochastic blockmodels and community structure in networks. Phys. Rev. E83, 016107 (2011). ArticleMathSciNetGoogle Scholar
- Bishop, C. M. Pattern Recognition and Machine Learning (Information Science and Statistics) (Springer, 2006).
- Mézard, M. & Montanari, A. Information, Physics, and Computation (Oxford Univ. Press, 2009).
- Decelle, A., Krzakala, F., Moore, C. & Zdeborová, L. Inference and phase transitions in the detection of modules in sparse networks. Phys. Rev. Lett.107, 065701 (2011). ArticleGoogle Scholar
- Kawamoto, T. Algorithmic detectability threshold of the stochastic block model. Phys. Rev. E97, 032301 (2018). ArticleGoogle Scholar
- Abbe, E. Community detection and stochastic block models: recent developments. Preprint at https://arxiv.org/abs/1703.10146 (2017).
- Peixoto, T. P. Bayesian stochastic blockmodeling. Preprint at https://arxiv.org/abs/1705.10225 (2017).
- Kawamoto, T. Algorithmic infeasibility of community detection in higher-order networks. Preprint at https://arxiv.org/abs/1710.08816 (2017).
- Kawamoto, T. & Kabashima, Y. Cross-validation estimate of the number of clusters in a network. Sci. Rep.7, 3327 (2017). ArticleGoogle Scholar
Acknowledgements
The authors thank H. Tokioka and S. Shinomoto for discussions. The authors are also grateful to J. Park and M. Rosvall for their comments. Finally, the authors appreciate all the people who contributed to the poll on the 2016 US presidential election and acknowledge support from the Faculty of Education in Kagawa University and the reunion of the faculty. T.K. was supported by JSPS (Japan) KAKENHI grant no. 26011023. T.A. was supported by the Research Institute for Mathematical Sciences, a joint research centre at Kyoto University, and open collaborative research at the National Institute of Informatics (NII) Japan (FY2017). T.K. and T.A. acknowledge financial support from JSPS KAKENHI grant no. 18K18604.
Author information
Authors and Affiliations
- Artificial Intelligence Research Center, National Institute of Advanced Industrial Science and Technology, Koto-ku, Tokyo, Japan Tatsuro Kawamoto
- Faculty of Education, Kagawa University, Takamatsu, Japan Takaaki Aoki
- Tatsuro Kawamoto







